IRT-based CAT selects each next item based on the examinee’s scored responses to all previous items. At the initial stages of a CAT, when only a single item or two has been administered, the next item is usually selected by a “step” rule – if the first item was answered correctly, the examinee’s original prior theta estimate is increased by some amount (e.g., .50); if the first item was answered incorrectly, the original theta estimate is decreased by the same amount. As the test proceeds and the examinee obtains a response pattern of at least one correct and one incorrect response,maximum likelihood estimation (MLE) is used to obtain a new theta estimate, which is based on the examinee’s responses to all administered items at that point in the test.

After each item is administered and scored, the new theta estimate is used to select the next item. That item is the unadministered item in the item bank that provides the most information at the current theta estimate. Figure 1 - 3 illustrate “maximum information” item selection in CAT. In addition to displaying information functions for 10 items, Figure 1 shows an initial theta estimate for a hypothetical examinee (indicated by the vertical line). This value is shown at 0.0, which is the mean of the theta scale. Values of information are computed for all items at that theta level. Figure 1 shows that Item 6 provides the most information of the 10 items at theta = 0.0. Therefore, Item 6 is administered and scored.

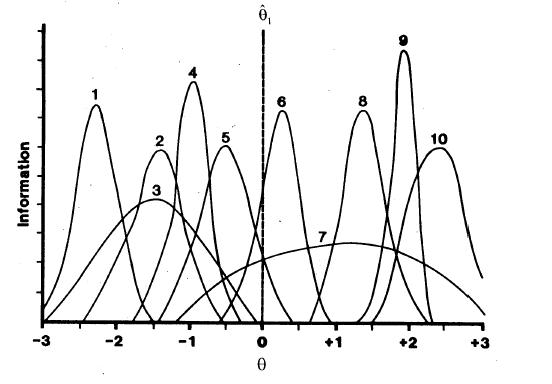
Based on that score (incorrect, in this example), a new theta estimate is determined (in this case using a step size of 1.0) as –1.0. Based on the maximum information item selection rule, Item 4 is administered (Figure 2), because it is the item at that theta level that has maximum information,and scored. Assuming that Item 4 was answered correctly, MLE can now be used to estimate theta.

Figure 2
Information Functions for 9 Items

The result is theta = -.50. Again,selecting an item by maximum information results in the selection of Item 5 (Figure 3). Scoring, theta estimation, and item selection continue until a termination criterion is reached.

Ending a CAT

One important characteristic of CAT is that the test termination criterion can be varied for different testing objectives. Some tests are used for selection or classification, for example to classify an individual as having mastered some domain of achievement or to select those who will be admitted to a school or college or hired for a job. Other tests are used for counseling or clinical purposes. The objective of such tests is to measure each individual as well as possible. In the context of CAT, these two objectives are operationalized by two different termination rules.

When CATs are not used for classification, a different termination rule applies. In this case, it is desirable to measure each examinee to a desired level of precision, as determined by a predetermined level of SEM. This will result in a set of “equiprecise” measurements, such that all examinees will have scores that are equivalently accurate – perhaps defining a new concept of “test fairness.” To implement equiprecise measurement, CAT allows the user to specify the level of SEM that is desired for each examinee. Assuming that the item bank has a sufficient number of test items properly distributed across the theta scale and the test is allowed to continue long enough for examinee, this goal will be achieved if the test is terminated when that level of SEM is reached.

A Sample CAT Report

Figure 4 shows the response record of a single examinee’s progress through a CAT. This CAT was designed to make a dichotomous classification around theta = 1.0 (1 standard deviation above the mean), with a plus or minus 1 standard error of measurement (SEM) band (a 68% confidence interval). The initial theta estimate (X) was 0.0 and the test item providing maximum information at that theta level was administered and answered correctly (C). The initial step size was 3.0 to attempt to force a mixed correct/incorrect) response pattern as quickly as possible, so the next item had maximum information at theta = 3.0. It, too, was answered correctly so additional difficult questions were given (Items 3 and 4) until an incorrect answer (I) was obtained. At that point, maximum likelihood estimation was used to obtain a theta estimate of 2.66. The item at that level (Item 5) was also answered incorrectly and the resulting theta estimate 1.87 with an SEM of .94. Note that each time a correct answer was obtained, the theta estimate increased, and an incorrect answer led to a decrease in estimated theta. Note also that the differences between successive estimated thetas decreased as the test proceeded, indicating that the test was converging on the examinee’s theta level; also, in general, the SEM tended to decrease, since additional item responses generally improve the estimation of theta.

In this test, the examinee’s estimated theta followed a downward trend, falling below the cut score of theta = 1.0 at Item 15. But the estimated theta could not be assumed to be reliably below that cut score because the SEM band still included theta = 1.0. So the test continued for another 10 items until the examinee’s estimated theta and its SEM were entirely below the cut score. This occurred at Item 20 (.55 + .43 = .98, which is just below 1.00) and the test was terminated. The test results indicate that this examinee’s estimated theta was below the cut score, with at least 68% confidence (actually, in this case because that confidence interval was symmetric and 50% was below the mean, the confidence level of a unidirectional decision would be 50% + 34% = 84%). Higher confidence could have been obtained by using a 2 SEM interval around estimated theta, which obviously would have a required a longer test.

Figure 4 also illustrates another characteristic of most CATs: As the test progresses, the examinee tends to alternate between correct and incorrect answers, as can be seen beginning with Item 7 or 8. This is the result of the convergence process that underlies CAT. The result, typically, is that each examinee will answer a set of questions on which he/she obtains 50% correct, even though each examinee will likely receive a set of questions of differing difficulty. In a sense, this characteristic of a CAT tends to equalize the #8220;psychological environment” of the test across examinees of different trait levels. By contrast, in a conventional test the examinee who is high on the trait will answer most items correctly and the low trait examinee will answer most of the items incorrectly.

Although this example is a CAT designed to make a dichotomous classification, the same principles would be observed in a CAT designed to measure each examinee to a prespecified level of precision (an "equiprecise "CAT). The only difference would be in the termination criterion. Rather than ending the CAT when the theta estimate was reliably below the cut score, an equiprecise CAT would end when the SEM associated with the theta estimate fell below a prespecified value (e.g., .20).

Lawrence Rudner has developed an excellent tutorial on CAT. In this tutorial you will have the opportunity to learn the logic of CAT and see the calculations that go on behind the scenes of an IRT-based CAT. You can interact with an actual CAT. The items and the correct answers are provided. You can try different scenarios and see what happens. You can pretend you are a high ability, average, or low ability examinee. You can intentionally miss easy items. You can get items correct that should be very difficult for you. Proceed to the CAT tutorial.

Additional resources on item response theory.